General Neural Gauge Fields
Fangneng Zhan, Lingjie Liu, Adam Kortylewski, Christian Theobalt
Max Planck Institute for Informatics, Germany
Physics Fields: 'Mass bends space.'
Neural Fields: 'Density bends space.'
Spherical Gauge Transform (DTU)
Planar Gauge Transform (DTU)
Abstract
The recent advance of neural fields, such as neural radiance fields, has significantly pushed the boundary of scene representation learning. Aiming to boost the computation efficiency and rendering quality of 3D scenes, a popular line of research maps the 3D coordinate system to another measuring system, e.g., 2D manifolds and hash tables, for modeling neural fields. The conversion of coordinate systems can be typically dubbed as gauge transformation, which is usually a pre-defined mapping function, e.g., orthogonal projection or spatial hash function. This begs a question: can we directly learn a desired gauge transformation along with the neural field in an end-to-end manner? In this work, we extend this problem to a general paradigm with a taxonomy of discrete and continuous cases, and develop an end-to-end learning framework to jointly optimize the gauge transformation and neural fields. To counter the problem that the learning of gauge transformations can collapse easily, we derive a general regularization mechanism from the principle of information conservation during the gauge transformation. To circumvent the high computation cost in gauge learning with regularization, we directly derive an information-invariant gauge transformation which allows to preserve scene information inherently and yield superior performance.
Gauge Transformations
In normal usage, a gauge defines a measuring system, e.g., pressure gauge and temperature gauge. Under the context of neural fields, a measuring system (i.e. gauge) is a specification of parameters to index a neural field,e.g., 3D Cartesian coordinate system, triplane in EG3D, hash table in Instant-NGP. The transformation between different measuring systems is dubbed as Gauge Transformation. The gauge transformation could be a pre-defined function. Intuitively, compared with a pre-defined function, a learnable gauge transformation is more favorable as it can be optimized towards the final use case of the neural field and possibly yields better performance. For learning neural gauge fields, we disambiguate between two cases: continuous (e.g., 2D plane and sphere surface) and discrete (e.g., hash table space) mappings.
1. Continuous Gauge Transformations

2. Discrete Gauge Transformations

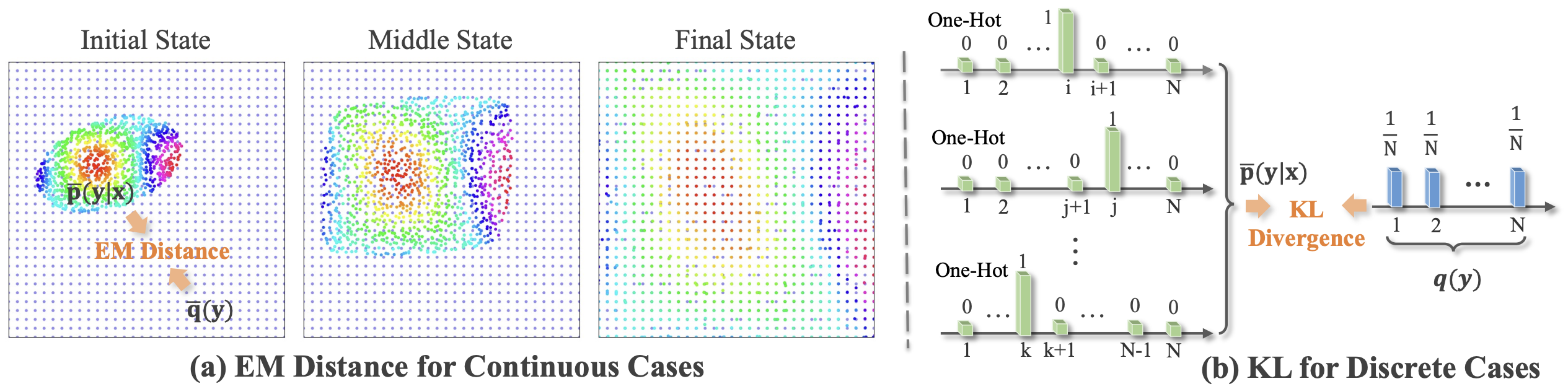
Regularization for Gauge Transformation
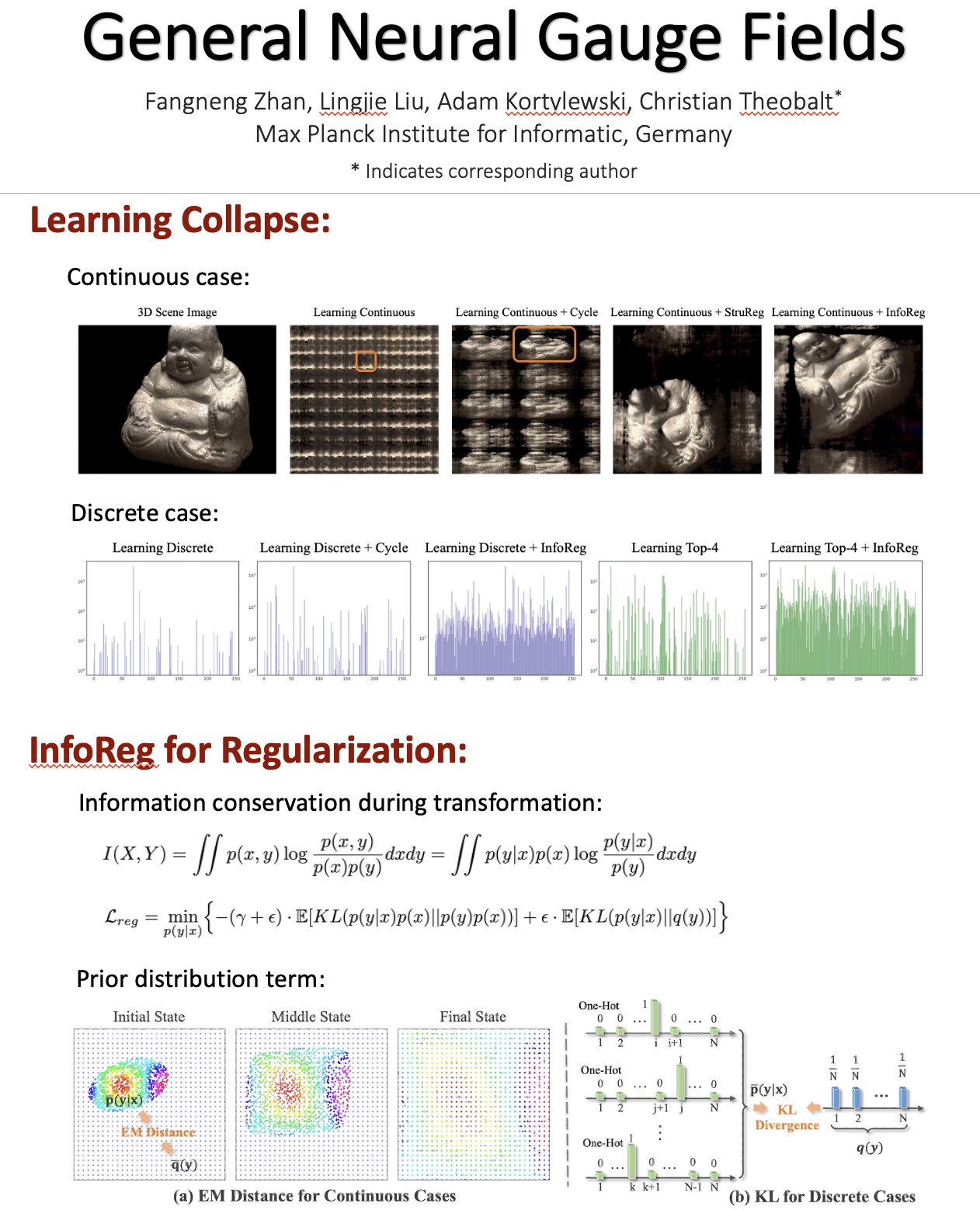
We found the learning of gauge transformations is easily stuck in local minimal. Specifically, the gauge transformation tends to collapse to a small region in continuous cases or collapse to a small number of indices in discrete cases, highlighting the need for an additional regularization to enable an effective learning of continuous and discrete gauge transformations.
More Results
UV Mapping

UV Editing